What does positive kurtosis mean?

Positive values of kurtosis indicate that a distribution is peaked and possess thick tails. Leptokurtic distributions have positive kurtosis values. A leptokurtic distribution has a higher peak and taller (i.e. fatter and heavy) tails than a normal distribution. An extreme positive kurtosis indicates a distribution where more of the values are located in the tails of the distribution rather than around the mean.

What is Kurtosis? | Simply Psychology

Q: What does a negative kurtosis mean?

Negative values of kurtosis indicate that a distribution is flat and has thin tails. Platykurtic distributions have negative kurtosis values. A platykurtic distribution is flatter (less peaked) when compared with the normal distribution, with fewer values in its shorter (i.e. lighter and thinner) tails.

What is Kurtosis?

By Dr. Saul McLeod, published 2019

What kurtosis tells us?

Kurtosis is a statistical measure used to describe the degree to which scores cluster in the tails or the peak of a frequency distribution. The peak is the tallest part of the distribution, and the tails are the ends of the distribution.

There are three types of kurtosis: mesokurtic, leptokurtic, and platykurtic.

Types of Kurtosis

Mesokurtic: Distributions that are moderate in breadth and curves with a medium peaked height.

Leptokurtic: More values in the distribution tails and more values close to the mean (i.e. sharply peaked with heavy tails)

Platykurtic: Fewer values in the tails and fewer values close to the mean (i.e. the curve has a flat peak and has more dispersed scores with lighter tails).

What kurtosis is normal?

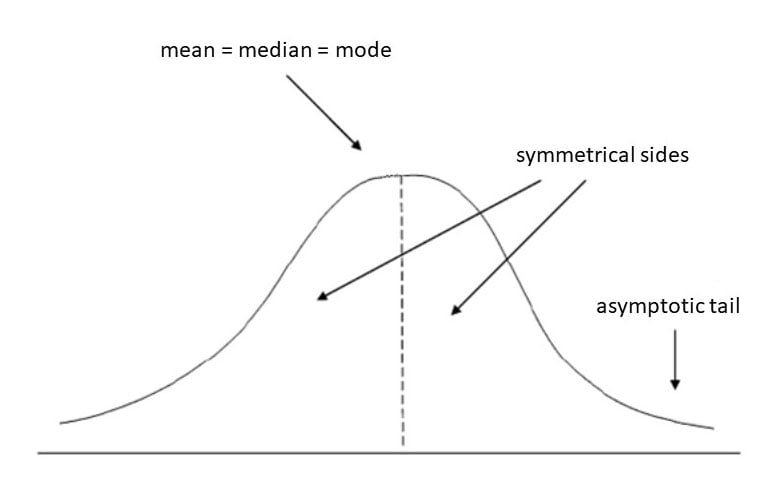
When kurtosis is equal to 3, the distribution is mesokurtic.

This means the kurtosis is the same as the normal distribution, it is mesokurtic (medium peak).

The kurtosis of a mesokurtic distribution is neither high nor low, rather it is considered to be a baseline for the two other classifications.

What does it mean when kurtosis is zero?

When kurtosis is equal to 0, the distribution is platykurtic.

A platykurtic distribution is flatter (less peaked) when compared with the normal distribution, with fewer values in its shorter (i.e. lighter and thinner) tails.

What does it mean when kurtosis is negative?

Negative excess values of kurtosis (<3) indicate that a distribution is flat and has thin tails. Platykurtic distributions have negative kurtosis values.

A platykurtic distribution is flatter (less peaked) when compared with the normal distribution, with fewer values in its shorter (i.e. lighter and thinner) tails.

What does it mean when kurtosis is positive?

Positive excess values of kurtosis (>3) indicate that a distribution is peaked and possess thick tails. Leptokurtic distributions have positive kurtosis values.

A leptokurtic distribution has a higher peak (thin bell) and taller (i.e. fatter and heavy) tails than a normal distribution.

An extreme positive kurtosis indicates a distribution where more of the values are located in the tails of the distribution rather than around the mean.

Further Information

The new definition of kurtosis measures "tailedness" rather than "peakedness" Shapes of Distributions (Kahn Academy) Normal Distribution (Bell Curve) What a p-value Tells You About Statistical Significance Statistics for Psychology

How to reference this article:

McLeod, S. A. (2019, Aug 13). What is kurtosis? Simply psychology: https://www.simplypsychology.org/kurtosis.html

Home | About Us | Privacy Policy | Advertise | Contact Us

Simply Psychology's content is for informational and educational purposes only. Our website is not intended to be a substitute for professional medical advice, diagnosis, or treatment.